#include <FermionBase.hpp>

Inheritance diagram for Xped::FermionBase< Symmetry_ >:

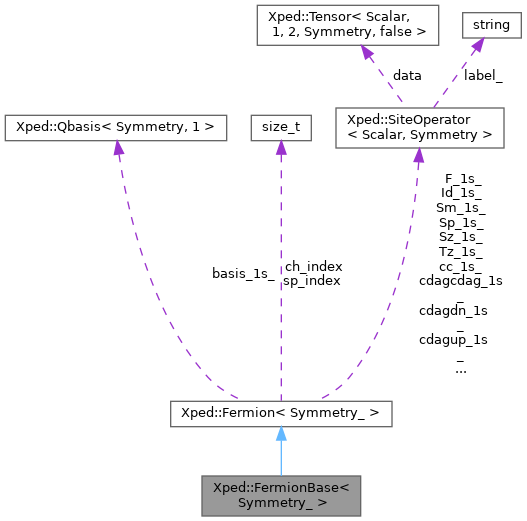
Collaboration diagram for Xped::FermionBase< Symmetry_ >:

[legend]

Public Types
using	Symmetry = Symmetry_

using	OperatorType = SiteOperator< Scalar, Symmetry >

using	OperatorTypeC = SiteOperator< std::complex< Scalar >, Symmetry >

using	qType = typename Symmetry::qType

Public Member Functions
	FermionBase ()=default

	FermionBase (std::size_t L_input, bool REMOVE_DOUBLE=false, bool REMVOVE_EMPTY=false, bool REMOVE_SINGLE=false)

std::size_t	dim () const

std::size_t	orbitals () const

OperatorType	Id (std::size_t orbital=0) const

Qbasis< Symmetry, 1 >	get_basis () const


template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), OperatorType >::type	c (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), OperatorType >::type	c (SPIN_INDEX sigma, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2() and!Dummy::IS_SPIN_SU2(), OperatorType >::type	c (SPIN_INDEX sigma, SUB_LATTICE G, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2() andDummy::IS_SPIN_SU2(), OperatorType >::type	c (SUB_LATTICE G, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), OperatorType >::type	cdag (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), OperatorType >::type	cdag (SPIN_INDEX sigma, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2() and!Dummy::IS_SPIN_SU2(), OperatorType >::type	cdag (SPIN_INDEX sigma, SUB_LATTICE G, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2() andDummy::IS_SPIN_SU2(), OperatorType >::type	cdag (SUB_LATTICE G, std::size_t orbital=0) const

OperatorType	sign (std::size_t orb1=0, std::size_t orb2=0) const

OperatorType	sign_local (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< true, OperatorType >::type	n (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type	n (SPIN_INDEX sigma, std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	d (std::size_t orbital=0) const

OperatorType	ns (std::size_t orbital=0) const

OperatorType	nh (std::size_t orbital=0) const


template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_SPIN_SU2(), OperatorType >::type	S (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_SPIN_SU2(), OperatorType >::type	Sdag (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type	Sz (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type	Sp (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type	Sm (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::NO_SPIN_SYM(), OperatorType >::type	Sx (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::NO_SPIN_SYM(), OperatorTypeC >::type	Sy (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::NO_SPIN_SYM(), OperatorType >::type	iSy (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type	Scomp (SPINOP_LABEL Sa, int orbital) const


template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2(), OperatorType >::type	T (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::IS_CHARGE_SU2(), OperatorType >::type	Tdag (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	Tz (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::NO_CHARGE_SYM(), OperatorType >::type	Tx (std::size_t orbital=0, SUB_LATTICE G=A) const

template<class Dummy = Symmetry>
std::enable_if< Dummy::NO_CHARGE_SYM(), OperatorType >::type	iTy (std::size_t orbital=0, SUB_LATTICE G=A) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	Tp (std::size_t orbital=0, SUB_LATTICE G=A) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	Tm (std::size_t orbital=0, SUB_LATTICE G=A) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	cc (std::size_t orbital=0) const

template<class Dummy = Symmetry>
std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type	cdagcdag (std::size_t orbital=0) const

Public Member Functions inherited from Xped::Fermion< Symmetry_ >
	Fermion ()

	Fermion (bool REMOVE_DOUBLE, bool REMOVE_EMPTY, bool REMOVE_SINGLE, bool CONSIDER_SPIN=true, bool CONSIDER_CHARGE=true)

OperatorType	Id_1s () const

OperatorType	F_1s () const

OperatorType	c_1s (SPIN_INDEX sigma) const

OperatorType	cdag_1s (SPIN_INDEX sigma) const

OperatorType	n_1s () const

OperatorType	n_1s (SPIN_INDEX sigma) const

OperatorType	ns_1s () const

OperatorType	nh_1s () const

OperatorType	d_1s () const

OperatorType	Sz_1s () const

OperatorType	Sp_1s () const

OperatorType	Sm_1s () const

OperatorType	Tz_1s () const

OperatorType	cc_1s () const

OperatorType	cdagcdag_1s () const

Qbasis< Symmetry, 1 >	basis_1s () const

Additional Inherited Members
Protected Member Functions inherited from Xped::Fermion< Symmetry_ >
void	fill_basis (bool REMOVE_DOUBLE, bool REMOVE_EMPTY, bool REMOVE_SINGLE)

void	fill_SiteOps (bool REMOVE_DOUBLE, bool REMOVE_EMPTY, bool REMOVE_SINGLE)

qType	getQ (SPIN_INDEX sigma, int Delta) const

qType	getQ (SPINOP_LABEL Sa) const

Protected Attributes inherited from Xped::Fermion< Symmetry_ >
Qbasis< Symmetry, 1 >	basis_1s_

std::unordered_map< std::string, std::pair< qType, std::size_t > >	labels

std::size_t	sp_index = 0

std::size_t	ch_index = 0

bool	HAS_SPIN

bool	HAS_CHARGE

OperatorType	Id_1s_

OperatorType	F_1s_

OperatorType	cup_1s_

OperatorType	cdn_1s_

OperatorType	cdagup_1s_

OperatorType	cdagdn_1s_

OperatorType	n_1s_

OperatorType	nup_1s_

OperatorType	ndn_1s_

OperatorType	d_1s_

OperatorType	Sz_1s_

OperatorType	Sp_1s_

OperatorType	Sm_1s_

OperatorType	Tz_1s_

OperatorType	cc_1s_

OperatorType	cdagcdag_1s_

Detailed Description

template<typename Symmetry_>
class Xped::FermionBase< Symmetry_ >

This class provides the local operators for fermions.

Member Typedef Documentation

◆ OperatorType

template<typename Symmetry_ >

using Xped::FermionBase< Symmetry_ >::OperatorType = SiteOperator<Scalar, Symmetry>

◆ OperatorTypeC

template<typename Symmetry_ >

using Xped::FermionBase< Symmetry_ >::OperatorTypeC = SiteOperator<std::complex<Scalar>, Symmetry>

◆ qType

template<typename Symmetry_ >

using Xped::FermionBase< Symmetry_ >::qType = typename Symmetry::qType

◆ Symmetry

template<typename Symmetry_ >

using Xped::FermionBase< Symmetry_ >::Symmetry = Symmetry_

Constructor & Destructor Documentation

◆ FermionBase() [1/2]

template<typename Symmetry_ >

Xped::FermionBase< Symmetry_ >::FermionBase ( )

default

◆ FermionBase() [2/2]

template<typename Symmetry >

Xped::FermionBase< Symmetry >::FermionBase	(	std::size_t	L_input,
		bool	REMOVE_DOUBLE = `false`,
		bool	REMVOVE_EMPTY = `false`,
		bool	REMOVE_SINGLE = `false`
	)

Parameters

L_input : the amount of orbitals

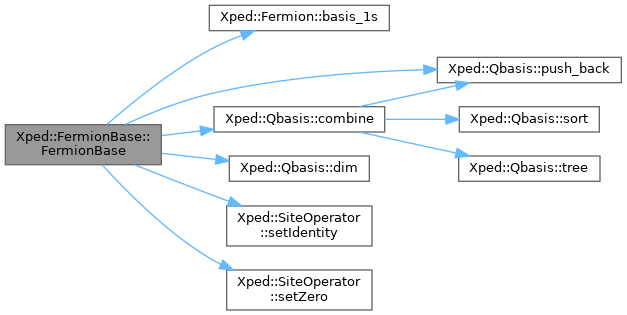
Here is the call graph for this function:

Member Function Documentation

◆ c() [1/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::c	(	SPIN_INDEX	sigma,
		std::size_t	orbital = `0`
	)		const

◆ c() [2/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2() and!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::c	(	SPIN_INDEX	sigma,
		SUB_LATTICE	G,
		std::size_t	orbital = `0`
	)		const

◆ c() [3/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::c ( std::size_t orbital = 0 ) const

Annihilation operator

Parameters

orbital : orbital index

Note: The annihilation spinor is build as follows \(c^{1/2} = \left( \begin{array}{c} -c_{\downarrow} \\ c_{\uparrow} \\ \end{array} \right)\) where the upper component corresponds to \( m=+1/2\) and the lower to \( m=-1/2\).

Here is the caller graph for this function:

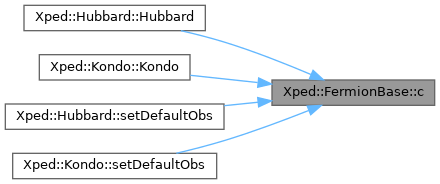
◆ c() [4/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2() andDummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::c	(	SUB_LATTICE	G,
		std::size_t	orbital = `0`
	)		const

◆ cc()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cc ( std::size_t orbital = 0 ) const

Orbital pairing η

Parameters

orbital : orbital index

Here is the caller graph for this function:

◆ cdag() [1/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cdag	(	SPIN_INDEX	sigma,
		std::size_t	orbital = `0`
	)		const

◆ cdag() [2/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2() and!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cdag	(	SPIN_INDEX	sigma,
		SUB_LATTICE	G,
		std::size_t	orbital = `0`
	)		const

◆ cdag() [3/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_SPIN_SU2() and!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cdag ( std::size_t orbital = 0 ) const

Creation operator.

Parameters

orbital : orbital index

Note: The creation spinor is computed as \( \left(c^{1/2}\right)^\dagger\). The definition of cdag which is consistent with this computation is: \(\left(c^{\dagger}\right)^{1/2} = \left( \begin{array}{c} c^\dagger_{\uparrow} \\ c^\dagger_{\downarrow} \\ \end{array} \right)\) where the upper component corresponds to \( m=+1/2\) and the lower to \( m=-1/2\).

Here is the caller graph for this function:

◆ cdag() [4/4]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2() andDummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cdag	(	SUB_LATTICE	G,
		std::size_t	orbital = `0`
	)		const

◆ cdagcdag()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::cdagcdag ( std::size_t orbital = 0 ) const

Orbital paring η†

Parameters

orbital : orbital index

Here is the caller graph for this function:

◆ d()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::d ( std::size_t orbital = 0 ) const

Double occupation

Parameters

orbital : orbital index

Here is the caller graph for this function:

◆ dim()

template<typename Symmetry_ >

std::size_t Xped::FermionBase< Symmetry_ >::dim ( ) const

inline

amount of states

◆ get_basis()

template<typename Symmetry_ >

Qbasis< Symmetry, 1 > Xped::FermionBase< Symmetry_ >::get_basis ( ) const

inline

Creates the full Hubbard Hamiltonian on the supersite with orbital-dependent U.

Parameters

U	: \(U\) for each orbital
Uph	: particle-hole symmetric \(U\) for each orbital (times \((n_{\uparrow}-1/2)(n_{\downarrow}-1/2)+1/4\))
Eorb	: \(\varepsilon\) onsite energy for each orbital
t	: \(t\)
V	: \(V\)
Vz	: \(V_z\)
Vxy	: \(V_{xy}\)
J	: \(J\) Returns the basis.

◆ Id()

template<typename Symmetry >

SiteOperator< double, Symmetry > Xped::FermionBase< Symmetry >::Id ( std::size_t orbital = 0 ) const

Identity

Here is the caller graph for this function:

◆ iSy()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::NO_SPIN_SYM(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::iSy ( std::size_t orbital = 0 ) const

Here is the call graph for this function:

Here is the caller graph for this function:

◆ iTy()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::NO_CHARGE_SYM(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::iTy	(	std::size_t	orbital = `0`,
		SUB_LATTICE	G = `A`
	)		const

Isospin y-component

Parameters

orbital : orbital index

Here is the call graph for this function:

◆ n() [1/2]

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::n	(	SPIN_INDEX	sigma,
		std::size_t	orbital = `0`
	)		const

◆ n() [2/2]

template<typename Symmetry >

template<typename Dummy >

std::enable_if< true, SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::n ( std::size_t orbital = 0 ) const

Occupation number operator

Parameters

orbital : orbital index

Here is the caller graph for this function:

◆ nh()

template<typename Symmetry >

SiteOperator< double, Symmetry > Xped::FermionBase< Symmetry >::nh ( std::size_t orbital = 0 ) const

Holon density \(n_h=2d-n-1=1-n_s\)

Parameters

orbital : orbital index

◆ ns()

template<typename Symmetry >

SiteOperator< double, Symmetry > Xped::FermionBase< Symmetry >::ns ( std::size_t orbital = 0 ) const

Spinon density \(n_s=n-2d\)

Parameters

orbital : orbital index

◆ orbitals()

template<typename Symmetry_ >

std::size_t Xped::FermionBase< Symmetry_ >::orbitals ( ) const

inline

amount of orbitals

◆ S()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::S ( std::size_t orbital = 0 ) const

Orbital spin

Parameters

orbital : orbital index

◆ Scomp()

template<typename Symmetry_ >

template<class Dummy = Symmetry>

std::enable_if<!Dummy::IS_SPIN_SU2(), OperatorType >::type Xped::FermionBase< Symmetry_ >::Scomp	(	SPINOP_LABEL	Sa,
		int	orbital
	)		const

inline

Here is the call graph for this function:

◆ Sdag()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Sdag ( std::size_t orbital = 0 ) const

Orbital spin†

Parameters

orbital : orbital index

Here is the caller graph for this function:

◆ sign()

template<typename Symmetry >

SiteOperator< double, Symmetry > Xped::FermionBase< Symmetry >::sign	(	std::size_t	orb1 = `0`,
		std::size_t	orb2 = `0`
	)		const

Fermionic sign for the hopping between two orbitals of nearest-neighbour supersites of a ladder.

Parameters

orb1	: orbital on supersite i
orb2	: orbital on supersite i+1

Here is the call graph for this function:

◆ sign_local()

template<typename Symmetry >

SiteOperator< double, Symmetry > Xped::FermionBase< Symmetry >::sign_local ( std::size_t orbital = 0 ) const

Fermionic sign for one orbital of a supersite.

Parameters

orbital : orbital index

◆ Sm()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Sm ( std::size_t orbital = 0 ) const

Here is the caller graph for this function:

◆ Sp()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Sp ( std::size_t orbital = 0 ) const

Here is the caller graph for this function:

◆ Sx()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::NO_SPIN_SYM(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Sx ( std::size_t orbital = 0 ) const

Here is the call graph for this function:

Here is the caller graph for this function:

◆ Sy()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::NO_SPIN_SYM(), SiteOperator< std::complex< double >, Symmetry > >::type Xped::FermionBase< Symmetry >::Sy ( std::size_t orbital = 0 ) const

Here is the call graph for this function:

Here is the caller graph for this function:

◆ Sz()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_SPIN_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Sz ( std::size_t orbital = 0 ) const

Here is the caller graph for this function:

◆ T()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::T ( std::size_t orbital = 0 ) const

Orbital Isospin

Parameters

orbital : orbital index

◆ Tdag()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Tdag ( std::size_t orbital = 0 ) const

Orbital Isospin†

Parameters

orbital : orbital index

◆ Tm()

template<typename Symmetry_ >

template<class Dummy = Symmetry>

std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type Xped::FermionBase< Symmetry_ >::Tm	(	std::size_t	orbital = `0`,
		SUB_LATTICE	G = `A`
	)		const

inline

Here is the call graph for this function:

◆ Tp()

template<typename Symmetry_ >

template<class Dummy = Symmetry>

std::enable_if<!Dummy::IS_CHARGE_SU2(), OperatorType >::type Xped::FermionBase< Symmetry_ >::Tp	(	std::size_t	orbital = `0`,
		SUB_LATTICE	G = `A`
	)		const

inline

Here is the call graph for this function:

◆ Tx()

template<typename Symmetry >

template<typename Dummy >

std::enable_if< Dummy::NO_CHARGE_SYM(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Tx	(	std::size_t	orbital = `0`,
		SUB_LATTICE	G = `A`
	)		const

Isospin x-component

Parameters

orbital : orbital index

Here is the call graph for this function:

◆ Tz()

template<typename Symmetry >

template<typename Dummy >

std::enable_if<!Dummy::IS_CHARGE_SU2(), SiteOperator< double, Symmetry > >::type Xped::FermionBase< Symmetry >::Tz ( std::size_t orbital = 0 ) const

Isospin z-component

Parameters

orbital : orbital index

Here is the call graph for this function:

The documentation for this class was generated from the following file:

include/Xped/Physics/FermionBase.hpp

Public Types

Public Member Functions

Additional Inherited Members

Detailed Description

Member Typedef Documentation

◆ OperatorType

◆ OperatorTypeC

◆ qType

◆ Symmetry

Constructor & Destructor Documentation

◆ FermionBase() [1/2]

◆ FermionBase() [2/2]

Member Function Documentation

◆ c() [1/4]

◆ c() [2/4]

◆ c() [3/4]

◆ c() [4/4]

◆ cc()

◆ cdag() [1/4]

◆ cdag() [2/4]

◆ cdag() [3/4]

◆ cdag() [4/4]

◆ cdagcdag()

◆ d()

◆ dim()

◆ get_basis()

◆ Id()

◆ iSy()

◆ iTy()

◆ n() [1/2]

◆ n() [2/2]

◆ nh()

◆ ns()

◆ orbitals()

◆ S()

◆ Scomp()

◆ Sdag()

◆ sign()

◆ sign_local()

◆ Sm()

◆ Sp()

◆ Sx()

◆ Sy()

◆ Sz()

◆ T()

◆ Tdag()

◆ Tm()

◆ Tp()

◆ Tx()

◆ Tz()