Namespaces
namespace	detail

namespace	DMRG

namespace	internal

namespace	IO

namespace	Log

namespace	mpi

namespace	Opts

namespace	PROP

namespace	random

namespace	Sym

namespace	treepair

namespace	util

Classes
class	AdjointOp

struct	ArrayMatrixLib

struct	ArrayTensorLib

struct	ArrayVectorLib

class	Basis

class	BlockUnaryOp

struct	Bool

class	CoeffBinaryOp

class	CoeffUnaryOp

struct	ctf_traits

struct	ctf_traits< CTF::Matrix< Scalar_ > & >

struct	ctf_traits< CTF::Matrix< Scalar_ > >

struct	ctf_traits< CTF::Tensor< Scalar_ > & >

struct	ctf_traits< CTF::Tensor< Scalar_ > >

class	CTM

class	CTMSolver

struct	CyclopsMatrixLib

struct	CyclopsTensorLib

struct	CyclopsVectorLib

class	DiagCoeffBinaryOp

class	DiagCoeffUnaryOp

struct	EigenMatrixLib

struct	EigenTensorLib

struct	EigenVectorLib

class	Energy

class	Fermion

class	Fermion< Sym::Combined< Sym::SU2< Sym::SpinSU2 >, Sym::SU2< Sym::SpinSU2 >, Symmetry_ > >

class	Fermion< Sym::Combined< Sym::SU2< Sym::SpinSU2 >, Symmetry_ > >

class	FermionBase

struct	FusionTree

struct	GaugeTriple

struct	HeapPolicy

class	Heisenberg

class	Hubbard

class	iPEPS

class	iPEPSIterator

struct	iPEPSSolverAD

struct	iPEPSSolverImag

class	Kondo

class	KondoNecklace

struct	MatrixInterface

class	Mps

struct	ObservableBase

struct	OneSiteObservable

struct	Param

struct	Pattern

struct	PlainInterface

struct	qarray

class	Qbasis

struct	ScalarTraits

struct	ScalarTraits< double >

struct	ScalarTraits< std::complex< RealScalar_ > >

class	SimpleUpdate

struct	SiteOperator

class	Spin

class	Spin< Sym::Combined< Sym::SU2< Sym::SpinSU2 >, Symmetry_ > >

class	Spin< Sym::SU2< Sym::SpinSU2 >, 0ul >

class	SpinBase

struct	StanArenaPolicy

struct	StorageType

class	Tensor

class	Tensor< Scalar_, Rank, CoRank, Symmetry_, false, AllocationPolicy_ >

class	Tensor< Scalar_, Rank, CoRank, Symmetry_, true, AllocationPolicy_ >

class	TensorBase

struct	TensorInterface

struct	TensorTraits

struct	TensorTraits< AdjointOp< XprType > >

struct	TensorTraits< BlockUnaryOp< XprType > >

struct	TensorTraits< CoeffBinaryOp< XprTypeLeft, XprTypeRight > >

struct	TensorTraits< CoeffUnaryOp< XprType, ReturnScalar > >

struct	TensorTraits< DiagCoeffBinaryOp< XprTypeLeft, XprTypeRight > >

struct	TensorTraits< DiagCoeffUnaryOp< XprType > >

struct	TensorTraits< Tensor< Scalar_, Rank_, CoRank_, Symmetry_, false, AllocationPolicy_ > >

class	TimePropagator

struct	TimeProtocol

struct	TMatrix

struct	TwoSiteObservable

struct	UnitCell

struct	VectorInterface

Typedefs
template<bool AD, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry , typename AllocationPolicy = HeapPolicy>
using	XTensor = std::conditional_t< AD, Tensor< Scalar, Rank, CoRank, Symmetry, true, AllocationPolicy >, Tensor< Scalar, Rank, CoRank, Symmetry, false, AllocationPolicy > >

template<bool AD, typename Scalar >
using	XScalar = std::conditional_t< AD, stan::math::var_value< Scalar >, Scalar >

template<typename Scalar >
using	VecOfMatIterator = internal::VecOfMatIterator< Scalar >

template<typename Index , Index oldVal, Index newVal, typename S >
using	seq_replace = seq::insert< seq::index_of< oldVal, S >, newVal, seq::remove< oldVal, S > >

template<size_t Nq>
using	qarray2 = std::array< qarray< Nq >, 2 >

template<size_t Nq>
using	qarray3 = std::array< qarray< Nq >, 3 >

template<size_t Nq>
using	qarray4 = std::array< qarray< Nq >, 4 >

template<typename Scalar >
using	MType = CTF::Matrix< Scalar >

template<typename Scalar >
using	cMType = const CTF::Matrix< Scalar >

template<typename Scalar >
using	MapMType = CTF::Matrix< Scalar >

template<typename Scalar >
using	cMapMType = const CTF::Matrix< Scalar >

using	MIndextype = int

using	Indextype = int

template<typename Scalar , std::size_t Rank>
using	TType = CTF::Tensor< Scalar >

template<typename Scalar , std::size_t Rank>
using	cTType = const CTF::Tensor< Scalar >

template<typename Scalar , std::size_t Rank>
using	MapTType = CTF::Tensor< Scalar >

template<typename Scalar , std::size_t Rank>
using	cMapTType = const CTF::Tensor< Scalar >

template<typename Scalar >
using	VType = CTF::Vector< Scalar >

typedef int	VIndextype

Enumerations
enum class	EFFICIENCY { MEMORY , TIME }

enum	SUB_LATTICE { A = 1 , B = -1 }

enum class	Kind { Fermion , Boson , Spin }

Functions
template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, Scalar, Rank, CoRank, Symmetry >	operator- (const Tensor< Scalar, Rank, CoRank, Symmetry, true > &t, Scalar s)

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, Scalar, Rank, CoRank, Symmetry >	operator+ (const Tensor< Scalar, Rank, CoRank, Symmetry, true > &t, Scalar s)

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, Scalar, Rank, CoRank, Symmetry >	operator* (const Tensor< Scalar, Rank, CoRank, Symmetry, true > &t, Scalar s)

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, Scalar, Rank, CoRank, Symmetry >	operator* (const Tensor< Scalar, Rank, CoRank, Symmetry, true > &t, stan::math::var_value< Scalar > s)

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry >	operator* (const Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &left, const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, true > &right)

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry >	operator* (const Tensor< Scalar, Rank, MiddleRank, Symmetry, true > &left, const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &right)

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >
XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry >	operator* (const Tensor< Scalar, Rank, MiddleRank, Symmetry, true > &left, const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, true > &right)

template<typename F >
void	reverse_pass_callback_alloc (F &&functor)

template<std::size_t depth, typename Symmetry >
std::ostream &	operator<< (std::ostream &os, const FusionTree< depth, Symmetry > &tree)

template<typename Symmetry , std::size_t depth, typename AllocationPolicy >
std::ostream &	operator<< (std::ostream &os, const Qbasis< Symmetry, depth, AllocationPolicy > &basis)

template<bool TRACK = false, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >
Tensor< std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry, false >	operator* (XPED_CONST Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &left, XPED_CONST Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &right)

template<bool TRACK = false, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >
Tensor< std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry, false >	operator* (Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &&left, Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &&right)

template<typename DerivedLeft , typename DerivedRight >
XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight >	operator+ (XPED_CONST TensorBase< DerivedLeft > &left, XPED_CONST TensorBase< DerivedRight > &right)

template<typename DerivedLeft , typename DerivedRight >
XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight >	operator+ (TensorBase< DerivedLeft > &&left, TensorBase< DerivedRight > &&right)

template<typename DerivedLeft , typename DerivedRight >
XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight >	operator- (XPED_CONST TensorBase< DerivedLeft > &left, XPED_CONST TensorBase< DerivedRight > &right)

template<typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator+ (XPED_CONST TensorBase< Derived > &left, Scalar offset)

template<typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator+ (Scalar offset, XPED_CONST TensorBase< Derived > &right)

template<typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator- (XPED_CONST TensorBase< Derived > &left, Scalar offset)

template<bool = false, typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator* (XPED_CONST TensorBase< Derived > &left, Scalar factor)

template<bool = false, typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator* (Scalar factor, XPED_CONST TensorBase< Derived > &right)

template<bool = false, typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator* (Scalar factor, TensorBase< Derived > &&right)

template<typename Derived , typename Scalar >
XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > >	operator/ (XPED_CONST TensorBase< Derived > &left, Scalar divisor)

template<typename Scalar , typename Symmetry >
Symmetry::Scalar	dot (XPED_CONST Mps< Scalar, Symmetry > &Bra, XPED_CONST Mps< Scalar, Symmetry > &Ket, const DMRG::DIRECTION DIR=DMRG::DIRECTION::RIGHT)

template<typename Scalar , typename Symmetry , typename AllocationPolicy >
void	contract_L (XPED_CONST Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &Bold, XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &Bra, XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &Ket, Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &Bnew)

template<typename Scalar , typename Symmetry , typename AllocationPolicy >
void	contract_R (XPED_CONST Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &Bold, XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &Bra, XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &Ket, Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &Bnew)

template<typename Scalar , typename Symmetry , std::size_t TRank, bool ENABLE_AD, Opts::CTMCheckpoint CPOpts, typename OpScalar , bool HERMITIAN>
TMatrix< std::conditional_t< ENABLE_AD, stan::math::var, typename OneSiteObservable< OpScalar, Symmetry, HERMITIAN >::ObsScalar > >	avg (XPED_CONST CTM< Scalar, Symmetry, TRank, ENABLE_AD, CPOpts > &env, OneSiteObservable< OpScalar, Symmetry, HERMITIAN > &op)

template<typename Scalar , typename Symmetry , std::size_t TRank, bool ENABLE_AD, Opts::CTMCheckpoint CPOpts, typename OpScalar , bool HERMITIAN>
std::array< TMatrix< std::conditional_t< ENABLE_AD, stan::math::var, typename TwoSiteObservable< OpScalar, Symmetry, HERMITIAN >::ObsScalar > >, 4 >	avg (XPED_CONST CTM< Scalar, Symmetry, TRank, ENABLE_AD, CPOpts > &env, TwoSiteObservable< OpScalar, Symmetry, HERMITIAN > &op)

std::ostream &	operator<< (std::ostream &os, const Pattern &pat)

template<typename Derived1 , typename Derived2 >
auto	decompose (XPED_CONST TensorBase< Derived1 > &T1, XPED_CONST TensorBase< Derived2 > &T2, const std::size_t max_nsv)

template<typename Scalar , typename Symmetry , typename AllocationPolicy >
std::pair< Tensor< Scalar, 1, 3, Symmetry, true, AllocationPolicy >, Tensor< Scalar, 3, 1, Symmetry, true, AllocationPolicy > >	decompose (XPED_CONST Tensor< Scalar, 3, 3, Symmetry, true, AllocationPolicy > &T1, XPED_CONST Tensor< Scalar, 3, 3, Symmetry, true, AllocationPolicy > &T2, const std::size_t max_nsv)

template<typename Scalar , typename Symmetry , typename AllocationPolicy >
std::pair< Tensor< Scalar, 1, 2, Symmetry, true, AllocationPolicy >, Tensor< Scalar, 2, 1, Symmetry, true, AllocationPolicy > >	decompose (XPED_CONST Tensor< Scalar, 2, 2, Symmetry, true, AllocationPolicy > &T1, XPED_CONST Tensor< Scalar, 2, 2, Symmetry, true, AllocationPolicy > &T2, const std::size_t max_nsv)

template<typename Scalar , typename Symmetry , typename AllocationPolicy , typename DerivedL , typename DerivedT , typename DerivedR , typename DerivedB >
Tensor< Scalar, 2, 3, Symmetry, false, AllocationPolicy >	applyWeights (XPED_CONST Tensor< Scalar, 2, 3, Symmetry, false, AllocationPolicy > &A, XPED_CONST TensorBase< DerivedL > &wL, XPED_CONST TensorBase< DerivedT > &wT, XPED_CONST TensorBase< DerivedR > &wR, XPED_CONST TensorBase< DerivedB > &wB)

template<typename Scalar , typename Symmetry , typename OtherScalar >
SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry >	operator* (OtherScalar s, XPED_CONST SiteOperator< Scalar, Symmetry > &op)

template<typename Scalar , typename Symmetry , typename OtherScalar >
SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry >	operator* (OtherScalar s, SiteOperator< Scalar, Symmetry > &&op)

template<typename Scalar , typename Symmetry , typename OtherScalar >
SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry >	operator* (XPED_CONST SiteOperator< Scalar, Symmetry > &op, OtherScalar s)

template<typename Scalar , typename Symmetry >
SiteOperator< Scalar, Symmetry >	operator* (XPED_CONST SiteOperator< Scalar, Symmetry > &O1, XPED_CONST SiteOperator< Scalar, Symmetry > &O2)

template<typename Scalar , typename Symmetry >
SiteOperator< Scalar, Symmetry >	operator+ (XPED_CONST SiteOperator< Scalar, Symmetry > &O1, XPED_CONST SiteOperator< Scalar, Symmetry > &O2)

template<typename Scalar , typename Symmetry >
SiteOperator< Scalar, Symmetry >	operator- (XPED_CONST SiteOperator< Scalar, Symmetry > &O1, XPED_CONST SiteOperator< Scalar, Symmetry > &O2)

template<typename Scalar , typename Symmetry >
SiteOperator< Scalar, Symmetry >	kroneckerProduct (XPED_CONST SiteOperator< Scalar, Symmetry > &O1, XPED_CONST SiteOperator< Scalar, Symmetry > &O2)

template<typename Scalar , typename Symmetry >
Tensor< Scalar, 2, 2, Symmetry, false >	tprod (XPED_CONST SiteOperator< Scalar, Symmetry > &O1, XPED_CONST SiteOperator< Scalar, Symmetry > &O2, bool ADD_TWIST=false, bool REVERSE_ORDER=false)

template<typename Scalar , typename Symmetry >
Tensor< Scalar, 2, 2, Symmetry, false >	tprod (SiteOperator< Scalar, Symmetry > &&O1, SiteOperator< Scalar, Symmetry > &&O2)

template<typename Scalar , typename Symmetry >
std::ostream &	operator<< (std::ostream &os, const SiteOperator< Scalar, Symmetry > &Op)

std::ostream &	operator<< (std::ostream &s, SPIN_INDEX sigma)

std::ostream &	operator<< (std::ostream &s, SUB_LATTICE sublat)

template<typename Symmetry >
qarray< Symmetry::Nq >	adjustQN (const qarray< Symmetry::Nq > &qin, const size_t number_cells, bool BACK=false)

template<size_t Nq>
bool	operator== (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
bool	operator!= (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
bool	operator<= (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
bool	operator>= (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
bool	operator< (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
bool	operator> (const qarray< Nq > &lhs, const qarray< Nq > &rhs)

template<size_t Nq>
qarray< Nq >	operator+ (const qarray< Nq > &a1, const qarray< Nq > &a2)

template<size_t Nq>
qarray< Nq >	operator- (const qarray< Nq > &a1, const qarray< Nq > &a2)

template<size_t Nq>
qarray< Nq >	operator* (const size_t &alpha, const qarray< Nq > &a)

template<std::size_t Nq1, std::size_t Nq2>
constexpr qarray< Nq1+Nq2 >	join (qarray< Nq1 > rhs, qarray< Nq2 > lhs)

template<std::size_t Nq1, std::size_t Nq2, std::size_t Nql>
std::pair< qarray< Nq1 >, qarray< Nq2 > >	disjoin (const qarray< Nql > &large_arr)

template<size_t Nq>
std::ostream &	operator<< (std::ostream &os, const qarray< Nq > &a)

template<size_t Nq>
qarray< Nq >	qplusinf ()
	‍*Constructs the vacuum (all quantum numbers equal to zero).‍/

template<size_t Nq>
qarray< Nq >	qminusinf ()

template<typename T , typename = typename std::enable_if_t<boost::describe::has_describe_enumerators<T>::value>>
std::ostream &	operator<< (std::ostream &os, const T &t)

template<typename T , typename = typename std::enable_if_t<boost::describe::has_describe_enumerators<T>::value>>
std::istream &	operator>> (std::istream &is, T &t)

std::ostream &	operator<< (std::ostream &os, const Basis &basis)

template<typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry , typename AllocationPolicy >
std::ostream &	operator<< (std::ostream &os, XPED_CONST Tensor< Scalar, Rank, CoRank, Symmetry, false, AllocationPolicy > &t)

template<typename Scalar , typename MTL , typename MTR >
MType< Scalar >	diagBinaryFunc (MTL &&M_left, const MTR &&M_right, const std::function< Scalar(Scalar, Scalar)> &func)

template<typename Scalar , typename MTL , typename MTR >
MType< Scalar >	binaryFunc (MTL &&M_left, const MTR &&M_right, const std::function< Scalar(Scalar, Scalar)> &func)

Typedef Documentation

◆ cMapMType

template<typename Scalar >

using Xped::cMapMType = typedef const CTF::Matrix<Scalar>

◆ cMapTType

template<typename Scalar , std::size_t Rank>

using Xped::cMapTType = typedef Eigen::TensorMap<cTType<Scalar, Rank> >

◆ cMType

template<typename Scalar >

using Xped::cMType = typedef const Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic>

◆ cTType

template<typename Scalar , std::size_t Rank>

using Xped::cTType = typedef const Eigen::Tensor<Scalar, Rank>

◆ Indextype

typedef Eigen::Index Xped::Indextype

◆ MapMType

template<typename Scalar >

using Xped::MapMType = typedef CTF::Matrix<Scalar>

◆ MapTType

template<typename Scalar , std::size_t Rank>

using Xped::MapTType = typedef Eigen::TensorMap<TType<Scalar, Rank> >

◆ MIndextype

typedef MatrixInterface::MIndextype Xped::MIndextype

◆ MType

template<typename Scalar >

using Xped::MType = typedef Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic>

◆ qarray2

template<size_t Nq>

using Xped::qarray2 = typedef std::array<qarray<Nq>, 2>

◆ qarray3

template<size_t Nq>

using Xped::qarray3 = typedef std::array<qarray<Nq>, 3>

◆ qarray4

template<size_t Nq>

using Xped::qarray4 = typedef std::array<qarray<Nq>, 4>

◆ seq_replace

template<typename Index , Index oldVal, Index newVal, typename S >

using Xped::seq_replace = typedef seq::insert<seq::index_of<oldVal, S>, newVal, seq::remove<oldVal, S> >

◆ TType

template<typename Scalar , std::size_t Rank>

using Xped::TType = typedef Eigen::Tensor<Scalar, Rank>

◆ VecOfMatIterator

template<typename Scalar >

using Xped::VecOfMatIterator = typedef internal::VecOfMatIterator<Scalar>

◆ VIndextype

typedef Eigen::Index Xped::VIndextype

◆ VType

template<typename Scalar >

using Xped::VType = typedef Eigen::Array<Scalar, Eigen::Dynamic, 1>

◆ XScalar

template<bool AD, typename Scalar >

using Xped::XScalar = typedef std::conditional_t<AD, stan::math::var_value<Scalar>, Scalar>

◆ XTensor

template<bool AD, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry , typename AllocationPolicy = HeapPolicy>

using Xped::XTensor = typedef std::conditional_t<AD, Tensor<Scalar, Rank, CoRank, Symmetry, true, AllocationPolicy>, Tensor<Scalar, Rank, CoRank, Symmetry, false, AllocationPolicy> >

Enumeration Type Documentation

◆ EFFICIENCY

enum class Xped::EFFICIENCY

strong

Enumerator
MEMORY
TIME

◆ Kind

enum class Xped::Kind

strong

Enumerator
Fermion
Boson
Spin

◆ SUB_LATTICE

enum Xped::SUB_LATTICE

Enumerator
A
B

Function Documentation

◆ adjustQN()

template<typename Symmetry >

qarray< Symmetry::Nq > Xped::adjustQN	(	const qarray< Symmetry::Nq > &	qin,
		const size_t	number_cells,
		bool	BACK = `false`
	)

◆ applyWeights()

template<typename Scalar , typename Symmetry , typename AllocationPolicy , typename DerivedL , typename DerivedT , typename DerivedR , typename DerivedB >

Tensor< Scalar, 2, 3, Symmetry, false, AllocationPolicy > Xped::applyWeights	(	XPED_CONST Tensor< Scalar, 2, 3, Symmetry, false, AllocationPolicy > &	A,
		XPED_CONST TensorBase< DerivedL > &	wL,
		XPED_CONST TensorBase< DerivedT > &	wT,
		XPED_CONST TensorBase< DerivedR > &	wR,
		XPED_CONST TensorBase< DerivedB > &	wB
	)

Here is the caller graph for this function:

◆ avg() [1/2]

template<typename Scalar , typename Symmetry , std::size_t TRank, bool ENABLE_AD, Opts::CTMCheckpoint CPOpts, typename OpScalar , bool HERMITIAN>

TMatrix< std::conditional_t< ENABLE_AD, stan::math::var, typename OneSiteObservable< OpScalar, Symmetry, HERMITIAN >::ObsScalar > > Xped::avg	(	XPED_CONST CTM< Scalar, Symmetry, TRank, ENABLE_AD, CPOpts > &	env,
		OneSiteObservable< OpScalar, Symmetry, HERMITIAN > &	op
	)

Here is the call graph for this function:

◆ avg() [2/2]

template<typename Scalar , typename Symmetry , std::size_t TRank, bool ENABLE_AD, Opts::CTMCheckpoint CPOpts, typename OpScalar , bool HERMITIAN>

std::array< TMatrix< std::conditional_t< ENABLE_AD, stan::math::var, typename TwoSiteObservable< OpScalar, Symmetry, HERMITIAN >::ObsScalar > >, 4 > Xped::avg	(	XPED_CONST CTM< Scalar, Symmetry, TRank, ENABLE_AD, CPOpts > &	env,
		TwoSiteObservable< OpScalar, Symmetry, HERMITIAN > &	op
	)

Here is the call graph for this function:

◆ binaryFunc()

template<typename Scalar , typename MTL , typename MTR >

MType< Scalar > Xped::binaryFunc	(	MTL &&	M_left,
		const MTR &&	M_right,
		const std::function< Scalar(Scalar, Scalar)> &	func
	)

◆ contract_L()

template<typename Scalar , typename Symmetry , typename AllocationPolicy >

void Xped::contract_L	(	XPED_CONST Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &	Bold,
		XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &	Bra,
		XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &	Ket,
		Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &	Bnew
	)

Here is the call graph for this function:

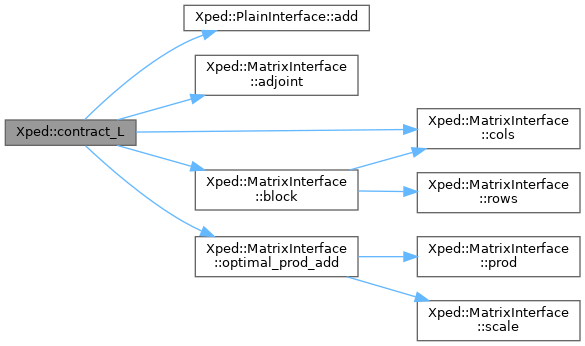
Here is the caller graph for this function:

◆ contract_R()

template<typename Scalar , typename Symmetry , typename AllocationPolicy >

void Xped::contract_R	(	XPED_CONST Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &	Bold,
		XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &	Bra,
		XPED_CONST Tensor< Scalar, 2, 1, Symmetry, false, AllocationPolicy > &	Ket,
		Tensor< Scalar, 1, 1, Symmetry, false, AllocationPolicy > &	Bnew
	)

Here is the call graph for this function:

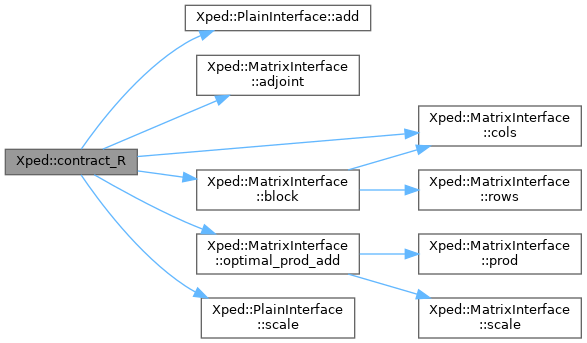
Here is the caller graph for this function:

◆ decompose() [1/3]

template<typename Scalar , typename Symmetry , typename AllocationPolicy >

std::pair< Tensor< Scalar, 1, 2, Symmetry, true, AllocationPolicy >, Tensor< Scalar, 2, 1, Symmetry, true, AllocationPolicy > > Xped::decompose	(	XPED_CONST Tensor< Scalar, 2, 2, Symmetry, true, AllocationPolicy > &	T1,
		XPED_CONST Tensor< Scalar, 2, 2, Symmetry, true, AllocationPolicy > &	T2,
		const std::size_t	max_nsv
	)

Here is the call graph for this function:

◆ decompose() [2/3]

template<typename Scalar , typename Symmetry , typename AllocationPolicy >

std::pair< Tensor< Scalar, 1, 3, Symmetry, true, AllocationPolicy >, Tensor< Scalar, 3, 1, Symmetry, true, AllocationPolicy > > Xped::decompose	(	XPED_CONST Tensor< Scalar, 3, 3, Symmetry, true, AllocationPolicy > &	T1,
		XPED_CONST Tensor< Scalar, 3, 3, Symmetry, true, AllocationPolicy > &	T2,
		const std::size_t	max_nsv
	)

Here is the call graph for this function:

◆ decompose() [3/3]

template<typename Derived1 , typename Derived2 >

auto Xped::decompose	(	XPED_CONST TensorBase< Derived1 > &	T1,
		XPED_CONST TensorBase< Derived2 > &	T2,
		const std::size_t	max_nsv
	)

Here is the call graph for this function:

◆ diagBinaryFunc()

template<typename Scalar , typename MTL , typename MTR >

MType< Scalar > Xped::diagBinaryFunc	(	MTL &&	M_left,
		const MTR &&	M_right,
		const std::function< Scalar(Scalar, Scalar)> &	func
	)

◆ disjoin()

template<std::size_t Nq1, std::size_t Nq2, std::size_t Nql>

std::pair< qarray< Nq1 >, qarray< Nq2 > > Xped::disjoin ( const qarray< Nql > & large_arr )

◆ dot()

template<typename Scalar , typename Symmetry >

Symmetry::Scalar Xped::dot	(	XPED_CONST Mps< Scalar, Symmetry > &	Bra,
		XPED_CONST Mps< Scalar, Symmetry > &	Ket,
		const DMRG::DIRECTION	DIR = `DMRG::DIRECTION::RIGHT`
	)

Here is the call graph for this function:

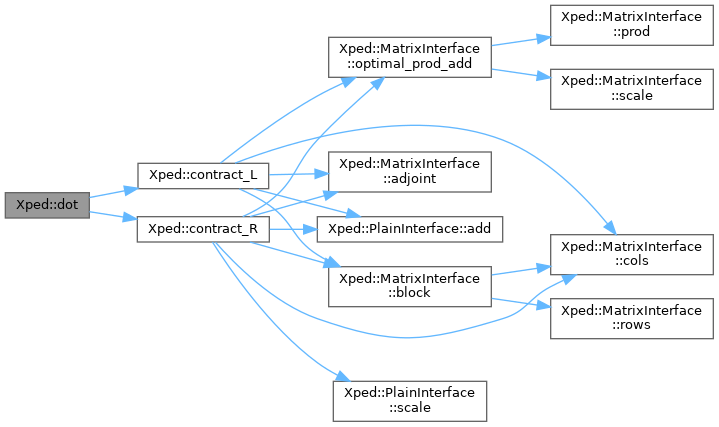
◆ join()

template<std::size_t Nq1, std::size_t Nq2>

constexpr qarray< Nq1+Nq2 > Xped::join	(	qarray< Nq1 >	rhs,
		qarray< Nq2 >	lhs
	)

constexpr

Join (concatenate) two qarrays.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ kroneckerProduct()

template<typename Scalar , typename Symmetry >

SiteOperator< Scalar, Symmetry > Xped::kroneckerProduct	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	O1,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	O2
	)

Here is the call graph for this function:

◆ operator!=()

template<size_t Nq>

bool Xped::operator!=	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

◆ operator*() [1/15]

template<size_t Nq>

qarray< Nq > Xped::operator*	(	const size_t &	alpha,
		const qarray< Nq > &	a
	)

Multiplies a qarray with a factor coefficient-wise.

◆ operator*() [2/15]

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, Scalar, Rank, CoRank, Symmetry > Xped::operator*	(	const Tensor< Scalar, Rank, CoRank, Symmetry, true > &	t,
		Scalar	s
	)

◆ operator*() [3/15]

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, Scalar, Rank, CoRank, Symmetry > Xped::operator*	(	const Tensor< Scalar, Rank, CoRank, Symmetry, true > &	t,
		stan::math::var_value< Scalar >	s
	)

◆ operator*() [4/15]

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry > Xped::operator*	(	const Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &	left,
		const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, true > &	right
	)

Here is the call graph for this function:

◆ operator*() [5/15]

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry > Xped::operator*	(	const Tensor< Scalar, Rank, MiddleRank, Symmetry, true > &	left,
		const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &	right
	)

Here is the call graph for this function:

◆ operator*() [6/15]

template<bool TRACK = true, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry > Xped::operator*	(	const Tensor< Scalar, Rank, MiddleRank, Symmetry, true > &	left,
		const Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, true > &	right
	)

◆ operator*() [7/15]

template<typename Scalar , typename Symmetry , typename OtherScalar >

SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry > Xped::operator*	(	OtherScalar	s,
		SiteOperator< Scalar, Symmetry > &&	op
	)

◆ operator*() [8/15]

template<typename Scalar , typename Symmetry , typename OtherScalar >

SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry > Xped::operator*	(	OtherScalar	s,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	op
	)

◆ operator*() [9/15]

template<bool = false, typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator*	(	Scalar	factor,
		TensorBase< Derived > &&	right
	)

◆ operator*() [10/15]

template<bool = false, typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator*	(	Scalar	factor,
		XPED_CONST TensorBase< Derived > &	right
	)

◆ operator*() [11/15]

template<bool TRACK = false, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >

Tensor< std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry, false > Xped::operator*	(	Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &&	left,
		Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &&	right
	)

◆ operator*() [12/15]

template<typename Scalar , typename Symmetry >

SiteOperator< Scalar, Symmetry > Xped::operator*	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	O1,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	O2
	)

Here is the call graph for this function:

◆ operator*() [13/15]

template<typename Scalar , typename Symmetry , typename OtherScalar >

SiteOperator< std::common_type_t< Scalar, OtherScalar >, Symmetry > Xped::operator*	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	op,
		OtherScalar	s
	)

◆ operator*() [14/15]

template<bool TRACK = false, typename Scalar , typename OtherScalar , std::size_t Rank, std::size_t MiddleRank, std::size_t CoRank, typename Symmetry >

Tensor< std::common_type_t< Scalar, OtherScalar >, Rank, CoRank, Symmetry, false > Xped::operator*	(	XPED_CONST Tensor< Scalar, Rank, MiddleRank, Symmetry, false > &	left,
		XPED_CONST Tensor< OtherScalar, MiddleRank, CoRank, Symmetry, false > &	right
	)

◆ operator*() [15/15]

template<bool = false, typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator*	(	XPED_CONST TensorBase< Derived > &	left,
		Scalar	factor
	)

◆ operator+() [1/7]

template<size_t Nq>

qarray< Nq > Xped::operator+	(	const qarray< Nq > &	a1,
		const qarray< Nq > &	a2
	)

Adds two qarrays coefficient-wise.

◆ operator+() [2/7]

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, Scalar, Rank, CoRank, Symmetry > Xped::operator+	(	const Tensor< Scalar, Rank, CoRank, Symmetry, true > &	t,
		Scalar	s
	)

◆ operator+() [3/7]

template<typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator+	(	Scalar	offset,
		XPED_CONST TensorBase< Derived > &	right
	)

◆ operator+() [4/7]

template<typename DerivedLeft , typename DerivedRight >

XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight > Xped::operator+	(	TensorBase< DerivedLeft > &&	left,
		TensorBase< DerivedRight > &&	right
	)

Here is the call graph for this function:

◆ operator+() [5/7]

template<typename Scalar , typename Symmetry >

SiteOperator< Scalar, Symmetry > Xped::operator+	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	O1,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	O2
	)

◆ operator+() [6/7]

template<typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator+	(	XPED_CONST TensorBase< Derived > &	left,
		Scalar	offset
	)

◆ operator+() [7/7]

template<typename DerivedLeft , typename DerivedRight >

XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight > Xped::operator+	(	XPED_CONST TensorBase< DerivedLeft > &	left,
		XPED_CONST TensorBase< DerivedRight > &	right
	)

◆ operator-() [1/5]

template<size_t Nq>

qarray< Nq > Xped::operator-	(	const qarray< Nq > &	a1,
		const qarray< Nq > &	a2
	)

Subtracts two qarrays coefficient-wise.

◆ operator-() [2/5]

template<bool TRACK = true, typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry >

XTensor< TRACK, Scalar, Rank, CoRank, Symmetry > Xped::operator-	(	const Tensor< Scalar, Rank, CoRank, Symmetry, true > &	t,
		Scalar	s
	)

◆ operator-() [3/5]

template<typename Scalar , typename Symmetry >

SiteOperator< Scalar, Symmetry > Xped::operator-	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	O1,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	O2
	)

◆ operator-() [4/5]

template<typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator-	(	XPED_CONST TensorBase< Derived > &	left,
		Scalar	offset
	)

◆ operator-() [5/5]

template<typename DerivedLeft , typename DerivedRight >

XPED_CONST CoeffBinaryOp< DerivedLeft, DerivedRight > Xped::operator-	(	XPED_CONST TensorBase< DerivedLeft > &	left,
		XPED_CONST TensorBase< DerivedRight > &	right
	)

◆ operator/()

template<typename Derived , typename Scalar >

XPED_CONST CoeffUnaryOp< Derived, std::common_type_t< typename Derived::Scalar, Scalar > > Xped::operator/	(	XPED_CONST TensorBase< Derived > &	left,
		Scalar	divisor
	)

◆ operator<()

template<size_t Nq>

bool Xped::operator<	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

Here is the caller graph for this function:

◆ operator<<() [1/10]

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const Basis &	basis
	)

◆ operator<<() [2/10]

template<std::size_t depth, typename Symmetry >

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const FusionTree< depth, Symmetry > &	tree
	)

Here is the call graph for this function:

Here is the caller graph for this function:

◆ operator<<() [3/10]

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const Pattern &	pat
	)

Here is the call graph for this function:

◆ operator<<() [4/10]

template<size_t Nq>

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const qarray< Nq > &	a
	)

◆ operator<<() [5/10]

template<typename Symmetry , std::size_t depth, typename AllocationPolicy >

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const Qbasis< Symmetry, depth, AllocationPolicy > &	basis
	)

Here is the call graph for this function:

◆ operator<<() [6/10]

template<typename Scalar , typename Symmetry >

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const SiteOperator< Scalar, Symmetry > &	Op
	)

Here is the call graph for this function:

◆ operator<<() [7/10]

template<typename T , typename = typename std::enable_if_t<boost::describe::has_describe_enumerators<T>::value>>

std::ostream & Xped::operator<<	(	std::ostream &	os,
		const T &	t
	)

◆ operator<<() [8/10]

template<typename Scalar , std::size_t Rank, std::size_t CoRank, typename Symmetry , typename AllocationPolicy >

std::ostream & Xped::operator<<	(	std::ostream &	os,
		XPED_CONST Tensor< Scalar, Rank, CoRank, Symmetry, false, AllocationPolicy > &	t
	)

◆ operator<<() [9/10]

std::ostream & Xped::operator<<	(	std::ostream &	s,
		SPIN_INDEX	sigma
	)

inline

◆ operator<<() [10/10]

std::ostream & Xped::operator<<	(	std::ostream &	s,
		SUB_LATTICE	sublat
	)

inline

◆ operator<=()

template<size_t Nq>

bool Xped::operator<=	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

◆ operator==()

template<size_t Nq>

bool Xped::operator==	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

◆ operator>()

template<size_t Nq>

bool Xped::operator>	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

◆ operator>=()

template<size_t Nq>

bool Xped::operator>=	(	const qarray< Nq > &	lhs,
		const qarray< Nq > &	rhs
	)

◆ operator>>()

template<typename T , typename = typename std::enable_if_t<boost::describe::has_describe_enumerators<T>::value>>

std::istream & Xped::operator>>	(	std::istream &	is,
		T &	t
	)

◆ qminusinf()

template<size_t Nq>

qarray< Nq > Xped::qminusinf ( )

◆ qplusinf()

template<size_t Nq>

qarray< Nq > Xped::qplusinf ( )

‍**Constructs the vacuum (all quantum numbers equal to zero).*‍/

◆ reverse_pass_callback_alloc()

template<typename F >

void Xped::reverse_pass_callback_alloc ( F && functor )

inline

Puts a callback on the autodiff stack to be called in reverse pass.

The intended use case is for the callable to ba a lambda function that captures any arguments it needs to work with. All captured values must be trivially destructible or they will leak memory! to_AD_stack() function can be used to ensure that.

Template Parameters

F	type of callable

Parameters

functor funtor or other callable to call in the reverse pass

Here is the caller graph for this function:

◆ tprod() [1/2]

template<typename Scalar , typename Symmetry >

Tensor< Scalar, 2, 2, Symmetry, false > Xped::tprod	(	SiteOperator< Scalar, Symmetry > &&	O1,
		SiteOperator< Scalar, Symmetry > &&	O2
	)

Here is the call graph for this function:

◆ tprod() [2/2]

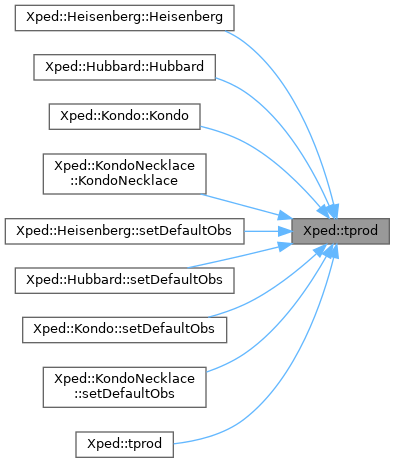
template<typename Scalar , typename Symmetry >

Tensor< Scalar, 2, 2, Symmetry, false > Xped::tprod	(	XPED_CONST SiteOperator< Scalar, Symmetry > &	O1,
		XPED_CONST SiteOperator< Scalar, Symmetry > &	O2,
		bool	ADD_TWIST = `false`,
		bool	REVERSE_ORDER = `false`
	)

Here is the call graph for this function:

Here is the caller graph for this function:

Namespaces

Classes

Typedefs

Enumerations

Functions

Typedef Documentation

◆ cMapMType

◆ cMapTType

◆ cMType

◆ cTType

◆ Indextype

◆ MapMType

◆ MapTType

◆ MIndextype

◆ MType

◆ qarray2

◆ qarray3

◆ qarray4

◆ seq_replace

◆ TType

◆ VecOfMatIterator

◆ VIndextype

◆ VType

◆ XScalar

◆ XTensor

Enumeration Type Documentation

◆ EFFICIENCY

◆ Kind

◆ SUB_LATTICE

Function Documentation

◆ adjustQN()

◆ applyWeights()

◆ avg() [1/2]

◆ avg() [2/2]

◆ binaryFunc()

◆ contract_L()

◆ contract_R()

◆ decompose() [1/3]

◆ decompose() [2/3]

◆ decompose() [3/3]

◆ diagBinaryFunc()

◆ disjoin()

◆ dot()

◆ join()

◆ kroneckerProduct()

◆ operator!=()

◆ operator*() [1/15]

◆ operator*() [2/15]

◆ operator*() [3/15]

◆ operator*() [4/15]

◆ operator*() [5/15]

◆ operator*() [6/15]

◆ operator*() [7/15]

◆ operator*() [8/15]

◆ operator*() [9/15]

◆ operator*() [10/15]

◆ operator*() [11/15]

◆ operator*() [12/15]

◆ operator*() [13/15]

◆ operator*() [14/15]

◆ operator*() [15/15]

◆ operator+() [1/7]

◆ operator+() [2/7]

◆ operator+() [3/7]

◆ operator+() [4/7]

◆ operator+() [5/7]

◆ operator+() [6/7]

◆ operator+() [7/7]

◆ operator-() [1/5]

◆ operator-() [2/5]

◆ operator-() [3/5]

◆ operator-() [4/5]

◆ operator-() [5/5]

◆ operator/()

◆ operator<()

◆ operator<<() [1/10]

◆ operator<<() [2/10]

◆ operator<<() [3/10]

◆ operator<<() [4/10]

◆ operator<<() [5/10]